Αλγόριθμος Prim

Σε αυτό το σεμινάριο, θα μάθετε πώς λειτουργεί ο Αλγόριθμος Prim. Επίσης, θα βρείτε λειτουργικά παραδείγματα του Αλγόριθμου Prim σε C, C ++, Java και Python.

Ο αλγόριθμος Prim είναι ένας ελάχιστος αλγόριθμος δέντρου που παίρνει ένα γράφημα ως είσοδο και βρίσκει το υποσύνολο των άκρων αυτού του γραφήματος που

σχηματίστε ένα δέντρο που περιλαμβάνει κάθε κορυφή
έχει το ελάχιστο άθροισμα βαρών μεταξύ όλων των δέντρων που μπορούν να σχηματιστούν από το γράφημα

Πώς λειτουργεί ο αλγόριθμος Prim

Εμπίπτει σε μια κατηγορία αλγορίθμων που ονομάζονται άπληστοι αλγόριθμοι που βρίσκουν το τοπικό βέλτιστο με την ελπίδα να βρουν ένα παγκόσμιο βέλτιστο.

Ξεκινάμε από μία κορυφή και συνεχίζουμε να προσθέτουμε άκρα με το χαμηλότερο βάρος μέχρι να φτάσουμε στον στόχο μας.

Τα βήματα για την εφαρμογή του αλγορίθμου Prim είναι τα εξής:

Αρχικοποιήστε το ελάχιστο δέντρο έκτασης με μια κορυφή επιλεγμένη τυχαία.
Βρείτε όλες τις άκρες που συνδέουν το δέντρο με νέες κορυφές, βρείτε το ελάχιστο και προσθέστε το στο δέντρο
Συνεχίστε να επαναλαμβάνετε το βήμα 2 έως ότου λάβουμε ένα ελάχιστο δέντρο έκτασης

Παράδειγμα αλγορίθμου Prim

Ξεκινήστε με ένα σταθμισμένο γράφημα

Επιλέξτε μια κορυφή

Επιλέξτε τη συντομότερη άκρη από αυτήν την κορυφή και προσθέστε την

Επιλέξτε την πλησιέστερη κορυφή που δεν βρίσκεται ακόμη στη λύση

Επιλέξτε την πλησιέστερη άκρη που δεν βρίσκεται ακόμη στη λύση, εάν υπάρχουν πολλές επιλογές, επιλέξτε μία τυχαία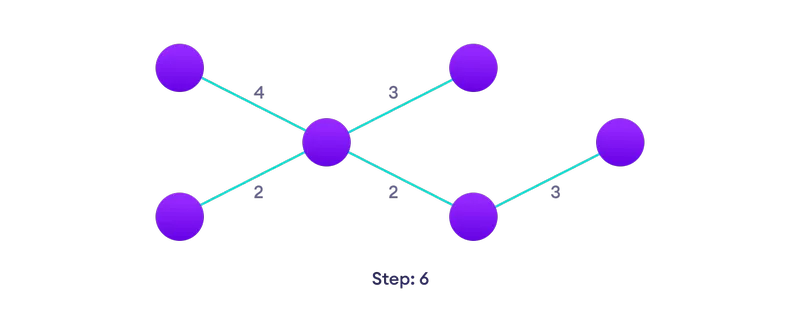

Επανάληψη έως ότου έχει ένα απλωμένο δέντρο

Ψευδοκώδικας Prim's Αλγόριθμος

Ο ψευδοκώδικας για τον αλγόριθμο του prim δείχνει πώς δημιουργούμε δύο σύνολα κορυφών U και VU. Το U περιέχει τη λίστα κορυφών που έχουν επισκεφτεί και VU τη λίστα κορυφών που δεν έχουν επισκεφτεί. Ένα προς ένα, μετακινούμε κορυφές από το σετ VU στο σετ U συνδέοντας το άκρο με το λιγότερο βάρος.

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

Παραδείγματα Python, Java και C / C ++

Αν και χρησιμοποιείται αναπαράσταση πίνακα γραφημάτων, ο αλγόριθμος αυτός μπορεί επίσης να εφαρμοστεί χρησιμοποιώντας Adjacency List για να βελτιώσει την αποτελεσματικότητά του.

Python Java C C ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

Αλγόριθμος Prim's vs Kruskal

Ο αλγόριθμος του Kruskal είναι ένας άλλος δημοφιλής αλγόριθμος ελάχιστου εύρους δέντρων που χρησιμοποιεί διαφορετική λογική για να βρει το MST ενός γραφήματος. Αντί να ξεκινά από μια κορυφή, ο αλγόριθμος του Kruskal ταξινομεί όλες τις άκρες από χαμηλό βάρος έως υψηλό και συνεχίζει να προσθέτει τις χαμηλότερες άκρες, αγνοώντας εκείνες τις ακμές που δημιουργούν έναν κύκλο.